Puzzle Club: Play Sudoku, Hanjie, Kakuro...

Logic & Number

Puzzle of the Day
Sudoku [Demo]
Kakuro [Demo]
Hanjie [Demo]
Killer Sudoku [Demo]
Futoshiki [Demo]
ABC Logic Puzzle
Jigsaw Sudoku [Demo]
Sudoku X [Demo]
Colour Hanjie
Calcudoku [Demo]
Fillomino
Killer Sudoku X [Demo]
Hidoku [Demo]
Extra Regions [Demo]
Battleships [Demo]
Odd/Even Sudoku [Demo]
Offset Sudoku [Demo]
Toroidal Sudoku [Demo]
Logi-5
Number Square [Demo]

Print Puzzles

Arrow Words
Bridges
Shikaku
Samurai Sudoku
SkyScraper Puzzles
16x16 Sudoku [Demo]

The PuzzleClub

Puzzle Tips
Edit Profile

Shikaku

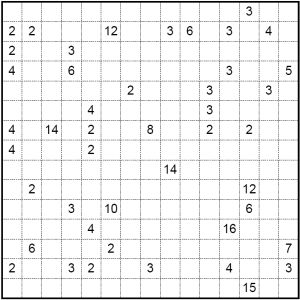
Shikaku is one of the latest puzzles to be added to the huge selection of number and logic puzzles here at the Puzzle Club. Here is what the start of the puzzle looks like: shikaku

As you can see, the shikaku grid is square and contains dotted lines going across and down that form a series of cells in the grid. All the puzzles on the puzzle club are actually on a 15 x 15 dotted grid. Each individual cell in the puzzle is ultimately a member of a rectangle containing just one number, and the sum total of the cells in the rectangle is the number that it incorporates.

Most cells in the start position of a shikaku don't contain any numbers, but those that do are the key. This tells you the size of the rectangle that contains that number - and there can only be one number in each rectangle. Thus a number '3' is either a member of a 3 x 1 rectangle or a 1 x 3 rectangle. Imagine that there are two threes, one place in row 1, column 1, and another placed in row 2, column 1. In this instance, we know the exact shape of the rectangle containing the '3' in r1c1: it must be a horizontal rectangle containing the first three cells of the puzzle, as each rectangle can only contain one number the rectangle cannot be oriented down.

Because exactly one cell in each solution rectangle is displayed in the start position, you will notice that the sum total of these givens is the number of cells in the puzzle - which is 225 (15 x 15) in the case of the puzzle club shikakus. Simply mark a bold border around the cells in each rectangle and keep going until you have worked out the shape of every rectangle in the puzzle and therefore to which rectangle each and every cell in the puzzle belongs.

Members can print off and play 20 shikaku puzzles in print ready PDF format complete with solution. These puzzles require simple logic alone to solve but are an unusual, fun and interesting addition to the puzzle range here at the puzzle club. Logged in members will now see links to the 20 shikaku PDFs.

Prefer to play puzzles in print? Take a look at the Book of Sikaku Puzzles.